Linear Regression
Model the linear relationship between numeric response and one or more explanatory variables by fitting a linear regression model.
Details
This module will create a linear model, modelling one dependent variable as a linear combination of one or more independent variables. It is important to note that linear regression assumes independence, linearity, normality and homoscedasticity of data. If these assumptions are violated, then the regression might be biased, thus it is important to test these assumptions before performing linear regression.
Linear regression is often fitted to the data in order to obtain a predictive model, which then can be used to estimate the value of response variable Y when only predictor (X) is known. Linear regression can also be used to assess the relationship between different variables in a data table and analyse whether the variance in some variables can be explained or modelled by linear combinations of other variables.
Output
The example below shows how to use the Linear Regression module to create a simple regression model of petal length (dependent/response variable) and petal width (predictor/independent variable).
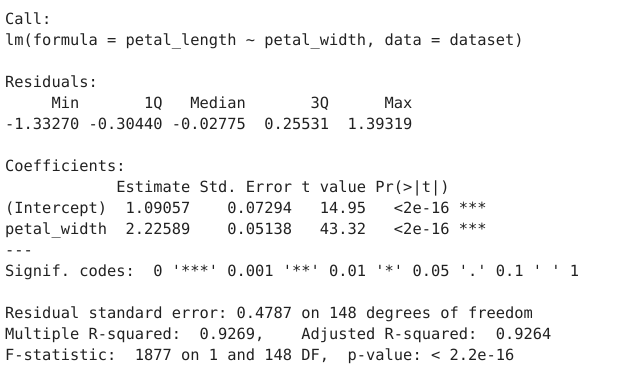
The output below shows the linear regression results. It also includes a graph of residuals plotted against the fitted values.
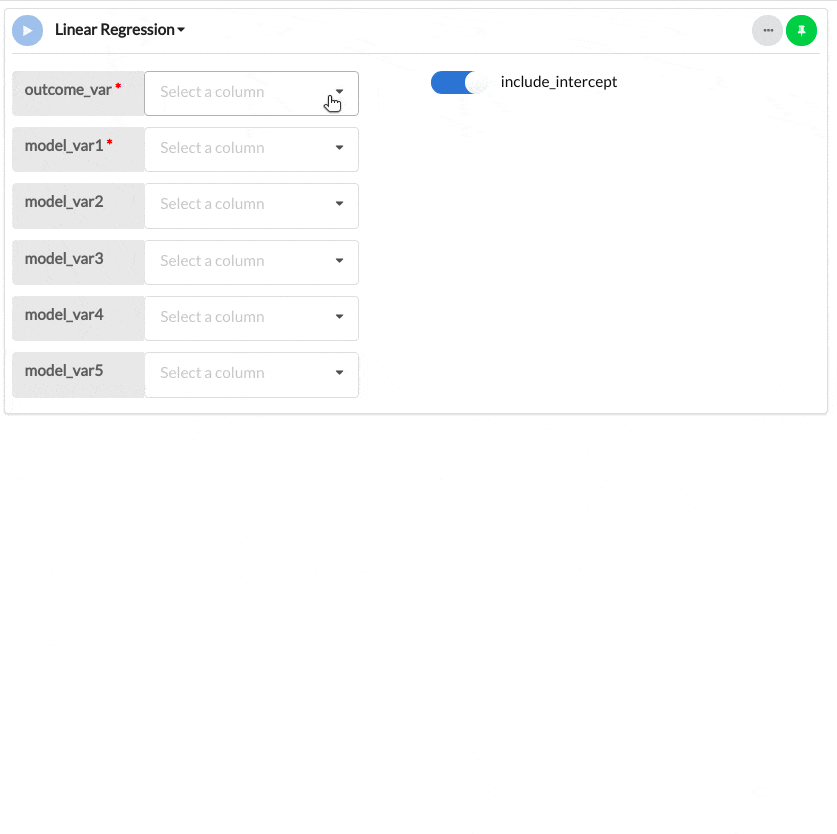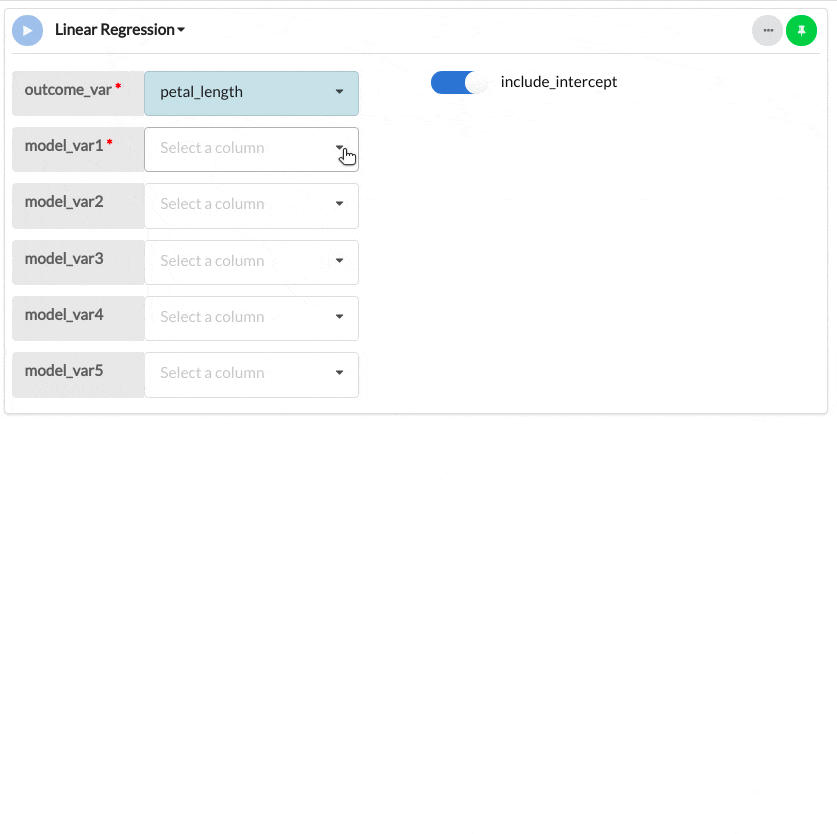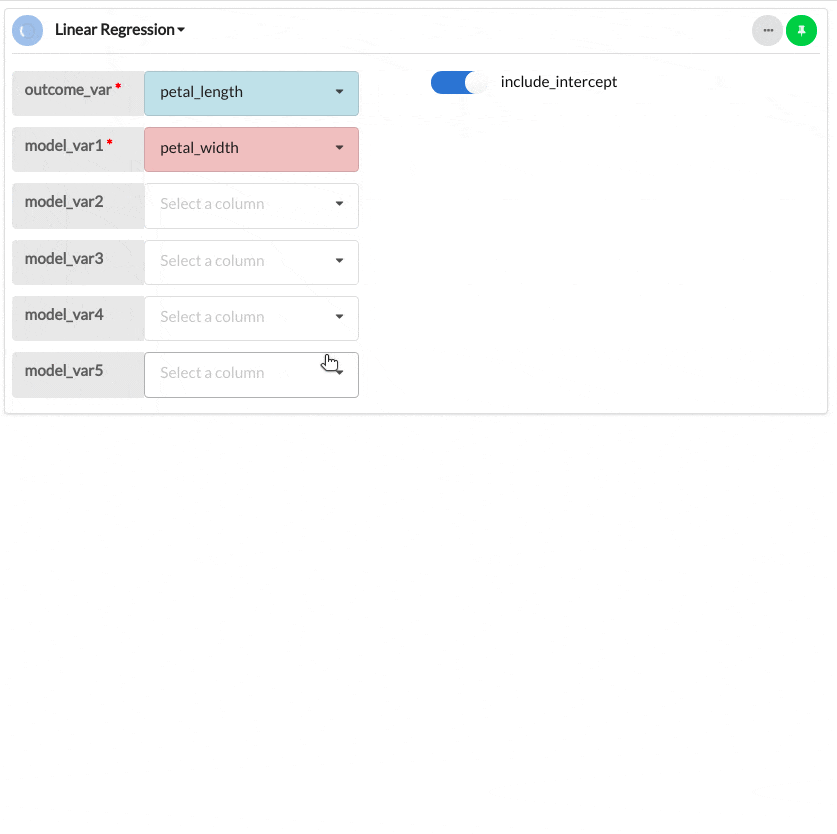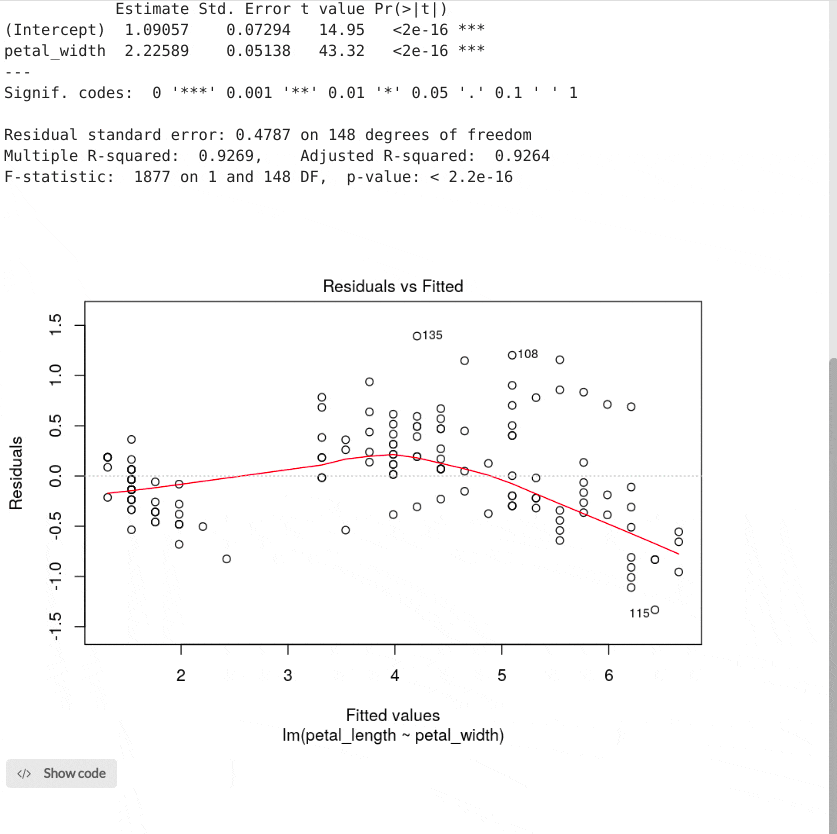
The module output is the summary of the linear model results. The summary function provides us with a wealth of information related to the linear model, including t-test, F-test, R-squared, residual, and significance values. More details on this can be found in the R documentation for lm.
From the example output, we see that the linear model intercept is equal to 1.09, and the petal width coefficient is equal to 2.23, thus we can write our linear equation as follows:
petal_length = 1.09 + 2.23 * petal_width
Parameters
| Variable name | Required | Constraints | Description |
|---|---|---|---|
| outcome_var | Yes | Column with data type one of: Decimal, Integer | The dependent variable to be modelled by the selections in model_var1, model_var2, ... |
| model_var1 | Yes | Any column other than the column chosen for outcome_var. | The first independent variable or predictor variable to include in the linear model. |
| model_var2 | No | Any column other than the column chosen for outcome_var. | An optional second predictor variable. |
| model_var3 | No | Any column other than the column chosen for outcome_var. | An optional third predictor variable. |
| model_var4 | No | Any column other than the column chosen for outcome_var. | An optional fourth predictor variable. |
| model_var5 | No | Any column other than the column chosen for outcome_var. | An optional fifth predictor variable. |
| include_intercept | Yes | Boolean | Whether to include an intercept term in the model |